Thomas Dybdahl Ahle

Hello, I'm Thomas. I lead the Foundational AI efforts at Normal Computing.

My research focuses on mechanistic interpretability and capabilities of large language models, the theoretical foundations of machine learning and massive data, including similarity search, hashing, high dimensional geometry, sketching and derandomization.

Research Resume Games Blog

Show All

Publications

[arxiv] In Review 2023 — NEW! Thermodynamic Linear Algebra Aifer, Donatella, Gordon, TA, Simpson, Crooks, Coles

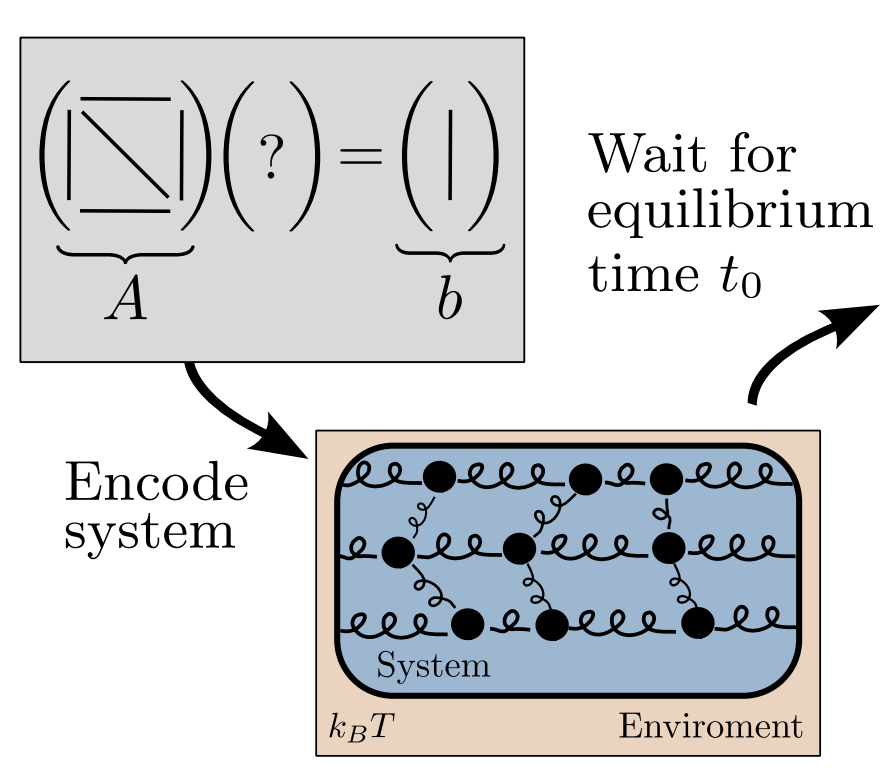
Linear algebraic primitives are at the core of many modern algorithms in engineering, science, and machine learning. Hence, accelerating these primitives with novel computing hardware would have tremendous economic impact. Quantum computing has been proposed for this purpose, although the resource requirements are far beyond current technological capabilities, so this approach remains long-term in timescale. Here we consider an alternative physics-based computing paradigm based on classical thermodynamics, to provide a near-term approach to accelerating linear algebra.
At first sight, thermodynamics and linear algebra seem to be unrelated fields. In this work, we connect solving linear algebra problems to sampling from the thermodynamic equilibrium distribution of a system of coupled harmonic oscillators. We present simple thermodynamic algorithms for (1) solving linear systems of equations, (2) computing matrix inverses, (3) computing matrix determinants, and (4) solving Lyapunov equations. Under reasonable assumptions, we rigorously establish asymptotic speedups for our algorithms, relative to digital methods, that scale linearly in matrix dimension. Our algorithms exploit thermodynamic principles like ergodicity, entropy, and equilibration, highlighting the deep connection between these two seemingly distinct fields, and opening up algebraic applications for thermodynamic computing hardware.
[arxiv] [github] [pdf] [poster] [website] NEURIPS 2023 — NEW! Clustering the Sketch: Dynamic Compression for Embedding Tables H Tsang, TA

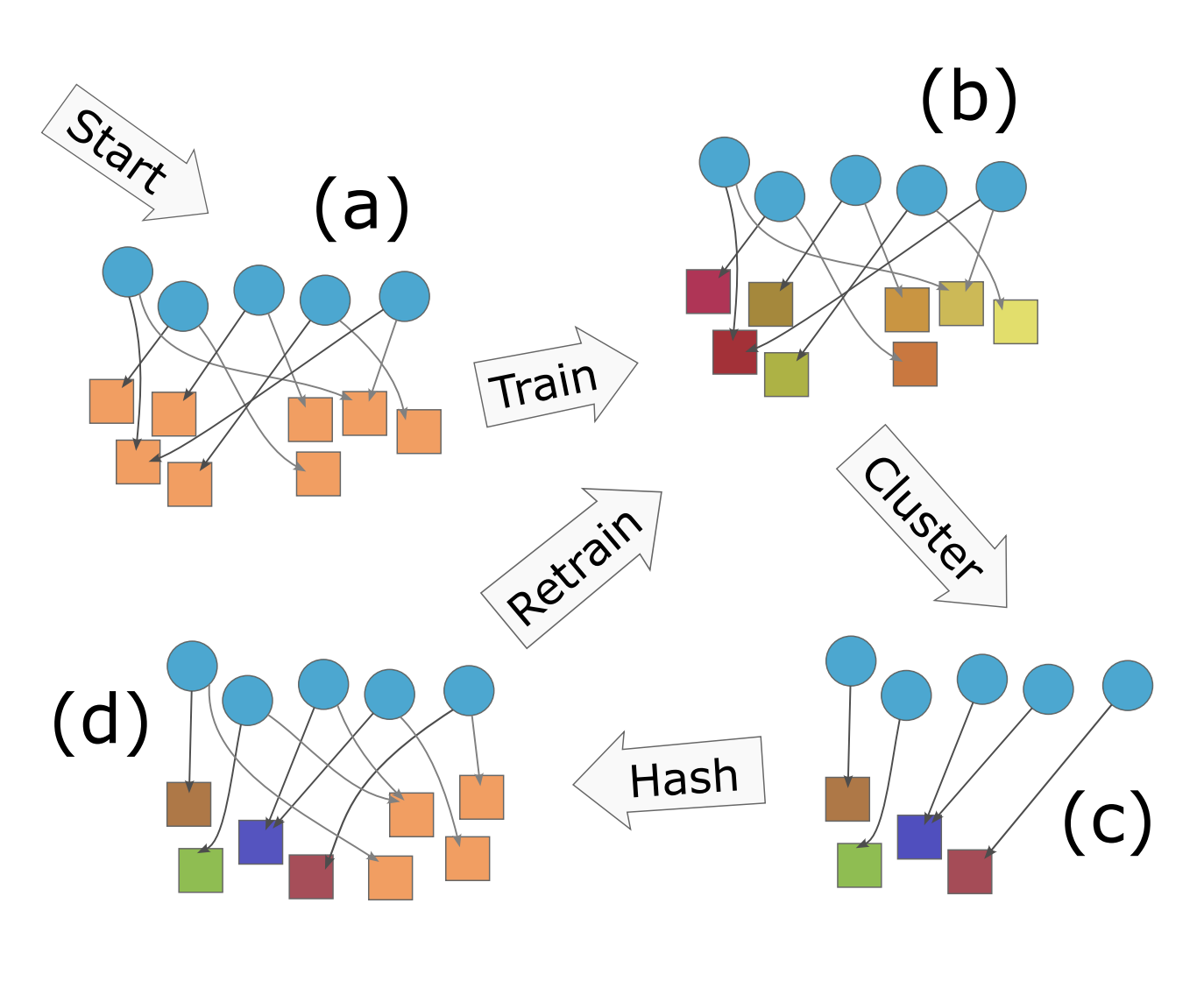
Embedding tables are used by machine learning systems to work with categorical features. These tables can become exceedingly large in modern recommendation systems, necessitating the development of new methods for fitting them in memory, even during training.

The best previous methods for table compression are so called "post training" quantization schemes such as "product" and "residual" quantization. These methods replace table rows with references to k-means clustered "codewords". Unfortunately, clustering requires prior knowledge of the table to be compressed, which limits the memory savings to inference time and not training time. Hence, recent work, like the QR method, has used random references (linear sketching), which can be computed with hash functions before training. Unfortunately, the compression achieved is inferior to that achieved by post-training quantization.

The new algorithm, CQR, shows how to get the best of two worlds by combining clustering and sketching: First IDs are randomly assigned to a codebook and codewords are trained (end to end) for an epoch. Next, we expand the codebook and apply clustering to reduce the size again. Finally, we add new random references and continue training.

We show experimentally close to those of post-training quantization with the training time memory reductions of sketch-based methods, and we prove that our method always converges to the optimal embedding table for least-squares training.
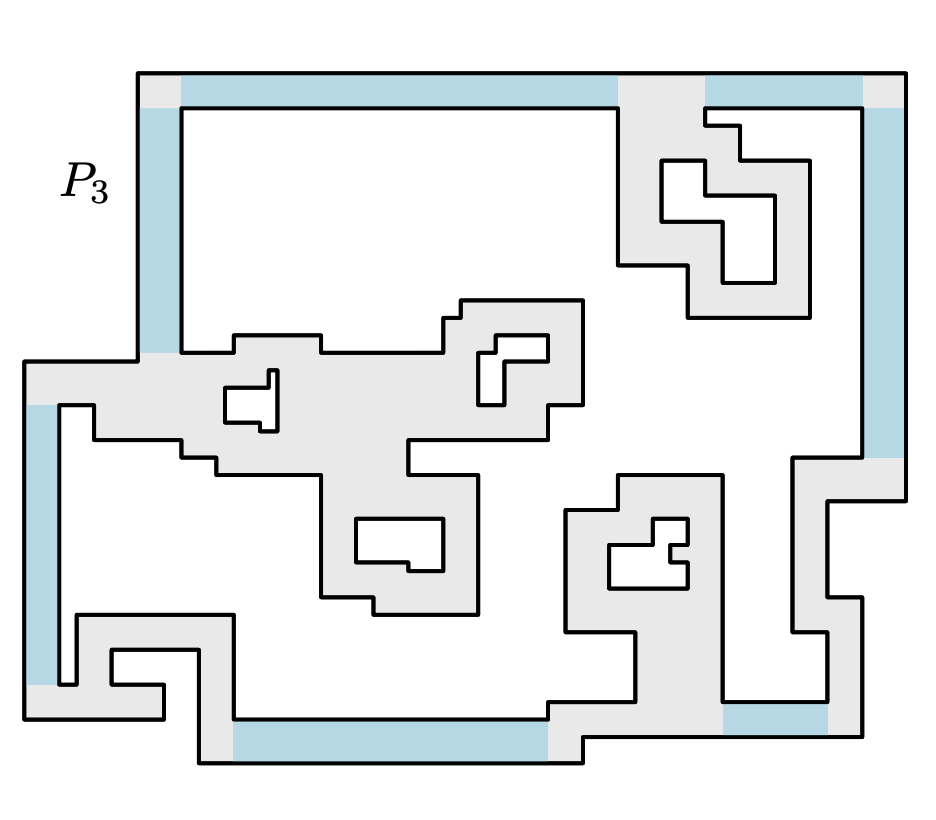
[arxiv] [pdf] [slides] SOCG 2022 Tiling with Squares and Packing Dominos in Polynomial Time A Aamand, M Abrahamsen, TA, P Rasmussen

We consider planar tiling and packing problems with polyomino pieces and a polyomino container P. A polyomino is a polygonal region with axis parallel edges and corners of integral coordinates, which may have holes. We give two polynomial time algorithms, one for deciding if P can be tiled with 2×2 squares (that is, deciding if P is the union of a set of non-overlapping copies of the 2×2 square) and one for packing P with a maximum number of non-overlapping and axis-parallel 2×1 dominos, allowing rotations of 90^∘. As packing is more general than tiling, the latter algorithm can also be used to decide if P can be tiled by 2×1 dominos.
These are classical problems with important applications in VLSI design, and the related problem of finding a maximum packing of 2×2 squares is known to be NP-Hard [J.~Algorithms 1990]. For our three problems there are known pseudo-polynomial time algorithms, that is, algorithms with running times polynomial in the area of P. However, the standard, compact way to represent a polygon is by listing the coordinates of the corners in binary. We use this representation, and thus present the first polynomial time algorithms for the problems. Concretely, we give a simple O(nlogn) algorithm for tiling with squares, and a more involved O(n⁴) algorithm for packing and tiling with dominos.
[arxiv] [journal] [pdf] STAT. PROB. LETT. 2022 Sharp and Simple Bounds for the raw Moments of the Binomial and Poisson Distributions TA

We prove the inequality E(X/μ)ᵏ ≤ [(k/μ)/log(k/μ+1)]ᵏ ≤ exp[k²/(2μ)] for sub−poissonian random variables, such as Binomially or Poisson distributed random variables with mean μ.

This improves over previous uniform bounds for the raw moments of those distributions by a factor exponential in k.
[arxiv] [pdf] [video] SISAP 2020 Similarity Search with Tensor Core Units TA, F Silvestri
Tensor Core Units (TCUs) are hardware accelerators developed for deep neural networks, which efficiently support the multiplication of two dense √m × √m matrices, where m is agiven hardware parameter. In this paper, we show that TCUs can speed up similarity searchproblems as well. We propose algorithms for the Johnson-Lindenstrauss dimensionality reduction and for similarity join that, by leveraging TCUs, achieve a √m speedup up with respect to traditional approaches.
[arxiv] [pdf] [video] SISAP 2020 On the Problem of p₁⁻¹ in Locality‑Sensitive Hashing TA
A Locality-Sensitive Hash (LSH) function is called (r,cr,p₁,p₁)-sensitive, if two data-points with a distance less than r collide with probability at least p₁ while data points with a distance greater than cr collide with probability at most p₂. These functions form the basis of the successful Indyk-Motwani algorithm (STOC 1998) for nearest neighbour problems. In particular one may build a c-approximate nearest neighbour data structure with query time O(n^ρ/p₁) where ρ = (log 1/p₁)/(log 1/p₂) ∈ (0,1). That is, sub-linear time, as long as p₁ is not too small. This is significant since most high dimensional nearest neighbour problems suffer from the curse of dimensionality, and can't be solved exact, faster than a brute force linear-time scan of the database.
Unfortunately, the best LSH functions tend to have very low collision probabilities, p₁ and p₂. Including the best functions for Cosine and Jaccard Similarity. This means that the n^ρ/p₁ query time of LSH is often not sub-linear after all, even for approximate nearest neighbours!
In this paper, we improve the general Indyk-Motwani algorithm to reduce the query time of LSH to O(n^ρ/p₁^1-ρ) (and the space usage correspondingly.) Since n^ρ/p₁^1-ρ < n ⇔ p₁ > 1/n, our algorithm always obtains sublinear query time, for all collision probabilities at least 1/n. For p₁ and p₂ small enough, our improvement over all previous methods can be up to a factor n in both query time and space.
The improvement comes from a simple change to the Indyk-Motwani algorithm, which can easily be implemented in existing software packages.
[arxiv] [blog post] [pdf] [slides] [video] FOCS 2020 Subsets and Supermajorities: Optimal Hashing‑based Set Similarity Search TA, J Knudsen

We formulate and optimally solve a new generalized Set Similarity Search problem, which assumes the size of the database and query sets are known in advance. By creating polylog copies of our data-structure, we optimally solve any symmetric Approximate Set Similarity Search problem, including approximate versions of Subset Search, Maximum Inner Product Search (MIPS), Jaccard Similarity Search and Partial Match.

Our algorithm can be seen as a natural generalization of previous work on Set as well as Euclidean Similarity Search, but conceptually it differs by optimally exploiting the information present in the sets as well as their complements, and doing so asymmetrically between queries and stored sets. Doing so we improve upon the best previous work: MinHash [J. Discrete Algorithms 1998], SimHash [STOC 2002], Spherical LSF [SODA 2016, 2017] and Chosen Path [STOC 2017] by as much as a factor n^.14 in both time and space; or in the near-constant time regime, in space, by an arbitrarily large polynomial factor.

Turning the geometric concept, based on Boolean supermajority functions, into a practical algorithm requires ideas from branching random walks on Z², for which we give the first non-asymptotic near tight analysis.

Our lower bounds follow from new hypercontractive arguments, which can be seen as characterizing the exact family of similarity search problems for which supermajorities are optimal. The optimality holds for among all hashing based data structures in the random setting, and by reductions, for 1 cell and 2 cell probe data structures. As a side effect, we obtain new hypercontractive bounds on the directed noise operator.
[arxiv] [pdf] [slides] [slides 2] SODA 2020 — Merged from "Almost Optimal Tensor Sketch" Oblivious Sketching of High‑Degree Polynomial Kernels TA, Kapralov, Knudsen, Pagh, Velingker, Woodruff, Zandieh

Kernel methods are fundamental tools in machine learning that allow detection of non-linear dependencies between data without explicitly constructing feature vectors in high dimensional spaces. A major disadvantage of kernel methods is their poor scalability: primitives such as kernel PCA or kernel ridge regression generally take prohibitively large quadratic space and (at least) quadratic time, as kernel matrices are usually dense. Some methods for speeding up kernel linear algebra are known, but they all invariably take time exponential in either the dimension of the input point set (e.g., fast multipole methods suffer from the curse of dimensionality) or in the degree of the kernel function.
Oblivious sketching has emerged as a powerful approach to speeding up numerical linear algebra over the past decade, but our understanding of oblivious sketching solutions for kernel matrices has remained quite limited, suffering from the aforementioned exponential dependence on input parameters. Our main contribution is a general method for applying sketching solutions developed in numerical linear algebra over the past decade to a tensoring of data points without forming the tensoring explicitly. This leads to the first oblivious sketch for the polynomial kernel with a target dimension that is only polynomially dependent on the degree of the kernel function, as well as the first oblivious sketch for the Gaussian kernel on bounded datasets that does not suffer from an exponential dependence on the dimensionality of input data points.
[arxiv] [pdf] [slides] FOCS 2017 — Updated Jun 2018 Optimal Las Vegas Locality Sensitive Data Structures TA

We show that approximate similarity (near neighbour) search can be solved in high dimensions with performance matching state of the art (data independent) Locality Sensitive Hashing, but with a guarantee of no false negatives. Specifically we give two data structures for common problems. For c-approximate near neighbour in Hamming space, for which we get query time dn^1/c+o(1) and space dn^1+1/c+o(1) matching that of [Indyk and Motwani, 1998] and answering a long standing open question from [Indyk, 2000a] and [Pagh, 2016] in the affirmative. For (s₁,s₂)-approximate Jaccard similarity we get query time d²n^ρ+o(1) and space d²n^1+ρ+o(1), ρ = ^{log(1+s₁)/(2s₁)}⁄_{log(1+s₂)/(2s₂)}, when sets have equal size, matching the performance of [Pagh and Christiani, 2017].

We use space partitions as in classic LSH, but construct these using a combination of brute force, tensoring and splitter functions à la [Naor et al., 1995]. We also show two dimensionality reduction lemmas with 1-sided error.
[arxiv] [pdf] [slides] SODA 2017 Parameter-free Locality‑Sensitive Hashing for Spherical Range Reporting TA, M Aumüller, R Pagh
We present a data structure for spherical range reporting on a point set S, i.e., reporting all points in S that lie within radius r of a given query point q. Our solution builds upon the Locality-Sensitive Hashing (LSH) framework of Indyk and Motwani, which represents the asymptotically best solutions to near neighbor problems in high dimensions. While traditional LSH data structures have several parameters whose optimal values depend on the distance distribution from q to the points of S, our data structure is parameter-free, except for the space usage, which is configurable by the user. Nevertheless, its expected query time basically matches that of an LSH data structure whose parameters have been optimally chosen for the data and query in question under the given space constraints. In particular, our data structure provides a smooth trade-off between hard queries (typically addressed by standard LSH) and easy queries such as those where the number of points to report is a constant fraction of S, or where almost all points in S are far away from the query point. In contrast, known data structures fix LSH parameters based on certain parameters of the input alone.

The algorithm has expected query time bounded by O(t(n/t)^ρ), where t is the number of points to report and ρ∈(0,1) depends on the data distribution and the strength of the LSH family used. We further present a parameter-free way of using multi-probing, for LSH families that support it, and show that for many such families this approach allows us to get expected query time close to O(n^ρ+t), which is the best we can hope to achieve using LSH. The previously best running time in high dimensions was Ω(tn^ρ). For many data distributions where the intrinsic dimensionality of the point set close to q is low, we can give improved upper bounds on the expected query time.
[arxiv] [pdf] [poster] [slides] PODS 2016 On the Complexity of Inner Product Similarity Join TA, R Pagh, I Razenshteyn, F Silvestri

A number of tasks in classification, information retrieval, recommendation systems, and record linkage reduce to the core problem of inner product similarity join (IPS join): identifying pairs of vectors in a collection that have a sufficiently large inner product. IPS join is well understood when vectors are normalized and some approximation of inner products is allowed. However, the general case where vectors may have any length appears much more challenging. Recently, new upper bounds based on asymmetric locality-sensitive hashing (ALSH) and asymmetric embeddings have emerged, but little has been known on the lower bound side. In this paper we initiate a systematic study of inner product similarity join, showing new lower and upper bounds. Our main results are:
* Approximation hardness of IPS join in subquadratic time, assuming the strong exponential time hypothesis.
* New upper and lower bounds for (A)LSH-based algorithms. In particular, we show that asymmetry can be avoided by relaxing the LSH definition to only consider the collision probability of distinct elements.
* A new indexing method for IPS based on linear sketches, implying that our hardness results are not far from being tight.

Our technical contributions include new asymmetric embeddings that may be of independent interest. At the conceptual level we strive to provide greater clarity, for example by distinguishing among signed and unsigned variants of IPS join and shedding new light on the effect of asymmetry.

Manuscripts

[arxiv] 2023 — NEW! Thermodynamic Matrix Exponentials and Thermodynamic Parallelism M Aifer, S Duffield, TA, P J Coles

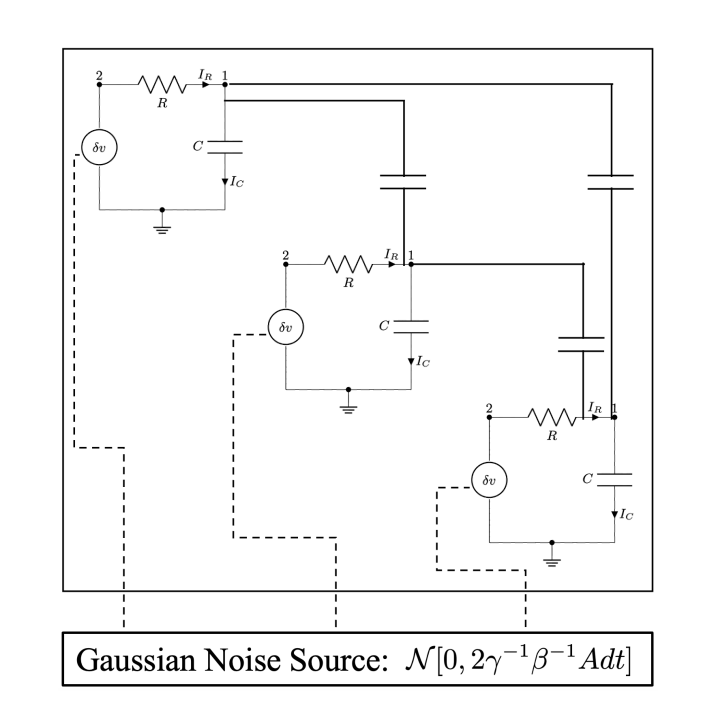
Thermodynamic computing exploits fluctuations and dissipation in physical systems to efficiently solve various mathematical problems. For example, it was recently shown that certain linear algebra problems can be solved thermodynamically, leading to an asymptotic speedup scaling with the matrix dimension. The origin of this "thermodynamic advantage" has not yet been fully explained, and it is not clear what other problems might benefit from it. Here we provide a new thermodynamic algorithm for exponentiating a real matrix, with applications in simulating linear dynamical systems. We describe a simple electrical circuit involving coupled oscillators, whose thermal equilibration can implement our algorithm. We also show that this algorithm also provides an asymptotic speedup that is linear in the dimension. Finally, we introduce the concept of thermodynamic parallelism to explain this speedup, stating that thermodynamic noise provides a resource leading to effective parallelization of computations, and we hypothesize this as a mechanism to explain thermodynamic advantage more generally.
[pdf] [video] 2022 Fast Variance Operator for Uncertainty Rating TA, S Karimi, P Tang
We introduce a principled approximate variance propagation framework for Bayesian Neural Networks. More accurate than Monte Carlo sampling, and much faster than previous variance propagation frameworks, it smoothly interpolates between quality and inference time. This is made possible by a new fast algorithm for updating a diagonal-plus-low-rank matrix approximation under various operations.

We tested our algorithm against sampling based MC Dropout and Variational Inference on a number of downstream uncertainty themed tasks, such as calibration and out-of-distribution testing. We find that Favour is as fast as performing 2-3 inference samples, while matching the performance of 10-100 samples.
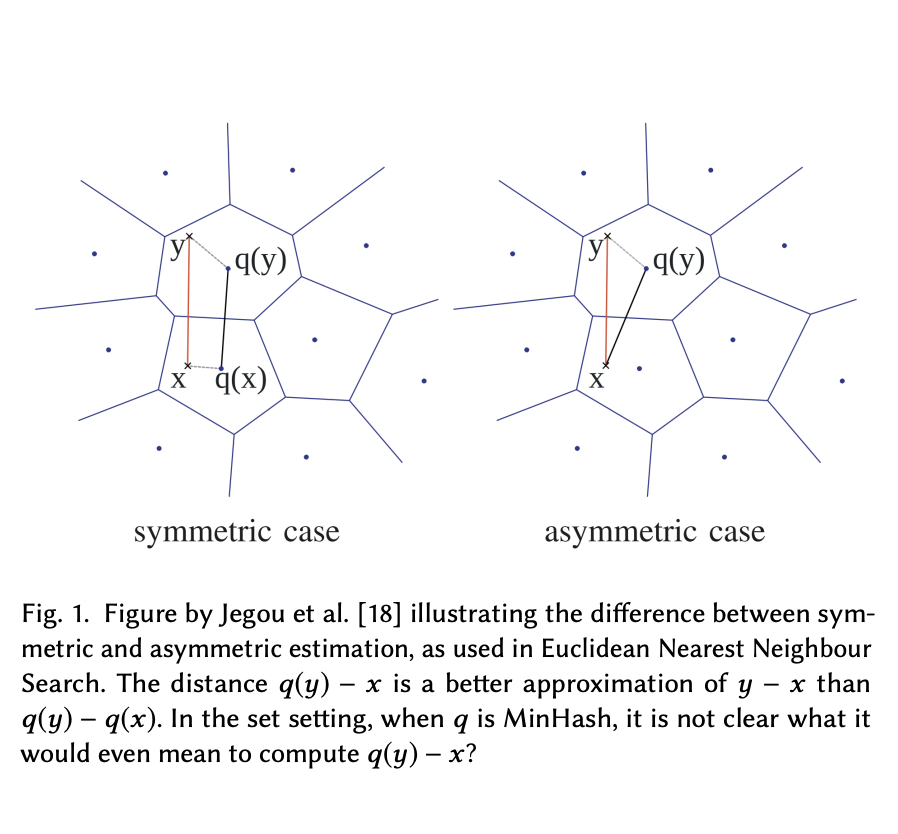
[pdf] [slides] 2021 Minner: Improved Similarity Estimation and Recall on MinHashed Databases TA

Quantization is the state of the art approach to efficiently storing and searching large high-dimensional datasets. Broder’97 introduced the idea of Minwise Hashing (MinHash) for quantizing or sketching large sets or binary strings into a small number of values and provided a way to reconstruct the overlap or Jaccard Similarity between two sets sketched this way.
In this paper, we propose a new estimator for MinHash in the case where the database is quantized, but the query is not. By computing the similarity between a set and a MinHash sketch directly, rather than first also sketching the query, we increase precision and improve recall.
We take a principled approach based on maximum likelihood with strong theoretical guarantees. Experimenal results show an improved recall@10 corresponding to 10-30% extra MinHash values. Finally, we suggest a third very simple estimator, which is as fast as the classical MinHash estimator while often more precise than the MLE.
Our methods concern only the query side of search and can be used with any existing MinHashed database without changes to the data.t
[arxiv] [pdf] 2021 — Updated May 2021 The Power of Hashing with Mersenne Primes TA, J Knudsen, M Thorup

The classic way of computing a k-universal hash function is to use a random degree-(k−1) polynomial over a prime field ℤ_p. For a fast computation of the polynomial, the prime p is often chosen as a Mersenne prime p = 2^b−1.
In this paper, we show that there are other nice advantages to using Mersenne primes. Our view is that the output of the hash function is a b-bit integer that is uniformly distributed in [2^b], except that p (the all 1s value) is missing. Uniform bit strings have many nice properties, such as splitting into substrings which gives us two or more hash functions for the cost of one, while preserving strong theoretical qualities. We call this trick “Two for one” hashing, and we demonstrate it on 4-universal hashing in the classic Count Sketch algorithm for second moment estimation.
We also provide a new fast branch-free code for division and modulus with Mersenne primes. Contrasting our analytic work, this code generalizes to Pseudo-Mersenne primes p = 2^b−c for small c, improving upon a classical algorithm of Crandall.
[arxiv] [pdf] 2019 — Merged into "Oblivious Sketching of High‑Degree Polynomial Kernels" Almost Optimal Tensor Sketch TA, J Knudsen
We construct a structured Johnson Lindenstrauss transformation that can be applied to simple tensors on the form x = x⁽¹⁾ ⊗ ... ⊗ x^(c) ∈ ℝ^dᶜ in time nearly c⋅d. That is, exponentially faster than writing out the Kronecker product and then mapping down. These matrices, M, which preserves the norm of any x ∈ ℝ^dᶜ, such that |‖Mx‖₂ - ‖x‖₂| < ε with probability 1-δ , can be taken to have just Õ(c² ε⁻² (log1/δ)³) rows. This is within c² (log 1/δ)² of optimal for any JL matrix [Larsen & Nelson], and improves upon earlier 'Tensor Sketch' constructions by Pagh and Pham, which used Õ(3ᶜ ε⁻² δ⁻¹) rows, by an exponential amount in both c and δ⁻² . It was shown by Avron, Nguyen and Woodruff that Tensor Sketch is a subspace embedding. This has a large number of applications, such as guaranteeing the correctness of kernel-linear regression performed directly on the reduced vectors. We show that our construction is a subspace embedding too, improving again upon the exponential dependency on c and δ⁻¹ , enabling sketching of much higher order polynomial kernels, such as Taylor approximations to the ubiquitous Gaussian radial basis function. Technically, we construct our matrix M such that M(x ⊗ y) = Tx ∘ T'y where ∘ is the Hadamard (element-wise) product and T and T' support fast matrix-vector multiplication ala [Ailon Chazelle]. To analyze the behavior of Mx on non-simple x , we show a higher order version of Khintchine's inequality, related to the higher order Gaussian chaos analysis by Latała. Finally we show that such sketches can be combined recursively, in a way that doesn't increase the dependency on c by much.
[pdf] 2017 It is NP-hard to verify an LSF on the sphere TA
We show a reduction from verifying that an LSF family `covers` the sphere, in the sense of Las Vegas LSF, to 3-sat.
[pdf] [slides] 2017 — Master thesis Minhash without false negatives TA
We consider efficient combinatorial constructions, that allow us to partly derandomize data-structures using the locality sensitive framework of Indyk and Motwani (FOCS '98). In particular our constructions allow us to make Zero-Error Probabilistic Polynomial Time (ZPP) analogues of two state of the art algorithms for `Approximate Set Similarity': This data-structure problem deals with storing a collection X of sets such that given a query set q for which there exists x ∈ P with |q ∩ x|/|q ∪ x| >= s_1 , the data structures return x'∈ P with |q ∩ x'|/|q ∪ x'|\ge s_2 . The first algorithm by Broder et al.introduced the famous `minhash' function, which in the locality sensitive framework yields an n^{ρ_b} time, n^{1+ρ_b} space data structure for ρ_b=(log1/s_1)/(log1/s_2) . The second by Christiani et al.~ gives an n^{ρ_c} time n^{1+ρ_c} space data-structure for ρ_c=(\log2s_1/(1+s_1))/(\log2s_2/(1+s_2)) . Both algorithms use Monte Carlo randomization, but we show that this is not necessary, at least up to n^{o(1)} factors. This settles an open problem from Arasu et al and Pagh asking whether locality sensitive data-structures could be made _exact_ or _without false negatives_ other than for hamming distance, and whether a performance gap was needed in the exponent. The main approach in the thesis is to replace the `locality sensitive hash functions' or `space partitions' with `combinatorial design'. We show that many such designs can be constructed efficiently with the `multi-splitters' introduced by Alon et al. We further show that careful constructions of such designs can be efficiently decoded. We also investigate upper and lower bounds on combinatorial analogues of the minhash algorithm. This is related to the existence of small, approximate minwise hashing families under l_∞ distance.
[pdf] 2017 Asymptotic Tail Bounds and Applications TA
In the field of Computer Science, the Chernoff bound is an extremely useful found bounding the error probabilities of various algorithms. Chernoff gives an exponentially decaying upper bound on the probability that a sum of independent random variables is many standard deviations away from its expectation. However sometimes we need more than an upper bound, and we need bounds that are tight within a constant factor or better. (There is a fairly standard tail lower bound, but it deviates from Chernoff by a factor of $\sqrt n$.) In this project I will explore and derive multiple upper and lower bounds for Chernoff using methods ranging from geometric series and generating functions to saddlepoint approximations and laplace approximation. All these results will be known, but they don’t seem have a good exposition in Computer Science. The reason also to consider more simple methods is to help an intuition for deriving similar bounds for different problems. In particular I will derive a tight bound for the size of the intersection between two hamming balls, which does not seem to exist in the literature. I will use the formulas to answer whether algorithms exists for the following problems: Locality Sensitive Filters in hamming space with limited use of random bits (as opposed to current methods, requiring gaussian samples), LSF with improved performance for low dimensional spaces. (dimension < 2 log n) Linear space bit sampling LSH, which I have previously partially analyzed, but only in a different context, in which a full analysis was not necessary.
[github] [pdf] 2013 — Bachelor thesis Donkeys to Monoids: A Computational Framework for Dynamic Semantics TA
In this paper I build a fully automatic system for translation of natural language into formal logic. I combine a variety of tools and theories to target standard issues such as anaphora resolution, sentence polarity etc. In particular I base my framework on dynamic logics in form of Dynamic Predicate Logic and a set of enhancements by Albert Visser (1999).
`Donkey Monoids', as I will call these monoidal DPL variants, are part of a movement in linguistics towards logics that can more naturally approximate human language in aspects such as polarity and scope. Indeed their name derives from the famous `Donkey Sentence' by Geach (1962) which exhibit these issues so well.
Visser didn't test his ideas computationally and neither did most people involved with DPL. In fact most of the classical literature on logification of natural language exhibits this `problem': Not testing computationally makes it easy to miss obvious details. With the present paper I supply such an experiment.
I build a rewriting system with a well defined set rules, discussing possible semantics. I apply the framework to a large collection of sentences, showing the conversion process step by step. Finally I discuss ways to enlarge the supported fragment of English, how we can combat and interpret the inherent ambiguity we meet, and how the flexibility of Donkey Monoids relate to the classical Montague lambda structures.

Research

Resume

Previously I ran Meta's "Machine Learning Efficiency" group, was the Chief of Machine Learning at the Natural Language Processing startup, SupWiz, and a Postdoctoral researcher in Theoretical Computer Science at the Basic Algorithms Research group (BARC) in Copenhagen with Mikkel Thorup. I did my PhD thesis with Rasmus Pagh on the Scalable Similarity Search project. Previous I worked with Oege de Moor and Samson Abramsky at the University of Oxford on Computational Linguistics; and with Eric Price at the University of Texas, Austin, on the fundamental limits of data-limited computation.

Media

Prosa — May 2021. "En ulv i fåreklæder."
Stibo — August 2016. "The Stibo-Foundation supports IT-talents."
Linux Format — January 2016. "Python: Sunfish chess engine." (pdf)
Computerworld — June 2015. "The National Team at the Programming World Cup."
Computerworld — October 2013. "Denmark's Three Greatest Programmers."

Games

Sunfish — a minimalist chess engine — play at Lichess
PyChess — a chess engine and Internet chess client — online version
Liar's Dice — a bluffing dice game based on Neural Counterfactual Regret. Play at dudo.ai and read the blog post.
numberlink — a generator and a fast solver for numberlink puzzles — play at Puzzle Baron
codenames — an AI that plays Codenames using word embeddings — play at Codewords.org
fastchess — an experiment into using the FastText library to play chess.
TrainBox — A train-based puzzle game

Programming Problems

These are various algorithmic challenges I set on the Sphere online judge.

POWTOW, TRANSFER, REALROOT, NANO, WAYHOME, VFRIENDS, VFRIEND2

Teaching

Practical Concurrent and Parallel Programming - 2019. MSc course on correct and efficient concurrent and parallel software, primarily using Java, on standard shared-memory multicore hardware.

Other

Memrise course for learning Danish through the most common 500 words.
Spejdrpedia — an online scout handbook